A Holistic Analysis Of Pythagoras Theorem Formula

Pythagoras Theorem
In the discipline of mathematics, the Pythagoras theorem holds immense significance and had unfolded different mysteries and areas of research in the triangle geometry. As the name signifies, the theorem was found by the Greek mathematician Pythagoras. The mathematician was born in the year 569 BC on the island of Samos, Greece. He has interjected an immense contribution in the field of mathematical subdivisions like polyhedral, areas, angles, polygons, triangles and other polygons. Not only limiting his contribution to academic mathematics, but he has also set many inventions and theories in musical mathematics. Among all these advances, his Pythagorean theorem is considered as the crucial point in the evolution of the present-day discipline of mathematics. Although he had made this much of advances in the field of mathematics, not many pieces of evidence are found regarding the implication of this theorem by the Babylonian mathematicians. Hence it could be deduced that his theorems were not well accepted by his contemporary colleagues. Because of his inventions, Pythagoras of Samos is nicknamed as the first pure mathematician. His theorem has been later researched by many of the specialists and currently, it has around 400 of its variations. There are many versions of the Pythagoras theorem published by different researchers, and to eliminate any confusion or anomaly we have provided a generic theorem in the below section
In a right-angled triangle, the total sum of the individual squares of the base and altitude would be equal to the square of the length of the hypotenuse.
Let us denote the base of the right-angled triangle as letter ‘b’, the altitude of the triangle as ‘a’ and hypotenuse of the same triangle as the letter ‘h’, then as per the Pythagoras theorem
h2 = b2 + a2
The numerical triplets which would satisfy this formula are termed as Pythagorean triples. The numerical triplets like (3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), etc. comes under the category of Pythagorean triplets. The multiples of these basic triplets also behave like a normal triplet, and if considered (a, b, c) as a basic Pythagorean triplet then the multiple of these triplets (ka, kb, kc) also comes under the category of the Pythagorean triplet. It should be noted that the constant ‘k’ in this context is a non-negative integer.
Evolution of the Pythagoras theorem
As mentioned earlier, the Pythagoras theorem formula is considered as one of the most renowned and path clearing concept in the history of mathematics. This theorem is so significant that even if today a student studying in high school is asked to state a theorem, it is most probable that he would state this theorem. Though the suspicions are being raised by the historians that there is a possibility that this theorem was being discovered by mathematicians and scholars in earlier times at different places.
If going down to the ancient history of India, the text Baudhayana Sulba Sutra, an ancient document discusses Mn of the Pythagorean triplets which were derived algebraically. These calculations were pertaining to the right-angled isosceles triangles. By utilizing the methodology of area computation, the numerical proof has been derived for the Pythagoras theorem in the document of Apastamba Sulba Sutra. These texts were confirmed to be drafted around the year of 600 BC. In the Chinese documents like Zhou Bi Suan Jing, the Pythagoras theorem is being and explained in a very efficient way.
If you search the mathematical research papers, you could come across derivations and explanation for the Pythagoras theorem. Scholars have stated that these numbers of derivations sum up to around 100. The oldest explanation is contemporary to the age of Euclid and the latest one dates to the 21st century. Below is provided one of the most accepted derivations for the Pythagoras theorem formula.
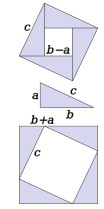
Proof: Consider a square in which four right-angled triangles with sides a, b, and c are arranged inwards along its perimeter so that the hypotenuse, c of the right-angled triangles turn out to be the side of the square. There would be a void in between the arrangements of the right-angled triangle which is in the shape of a square with side b-a. From the below diagram it would be evident that the area of each triangle would be equal to ½ ab.
Algebraically, the area of the whole square considering the dimensions of the triangles and inner square would be
(b-a)2 + (4/2) ab = a2 + b2
It is also clear that the actual length of the square is c and hence they are of the square would be c2
Hence c2 = a2 + b2
Augmented studies on this theorem
As per the principles of mathematics and its subsidiaries, a comprehensive theorem is the one that brings the way to the innovation of new theorems. The Pythagoras theorem had even led to the generation of a new subtopic in mathematics, trigonometry. The scope of mathematics is very large and had been the basis of many scientifically and mathematically diverse theorems.
A set of numerical triplets would be termed as the primitive Pythagorean triplet if their GCD is 1. To prove this statement, let us look at the theorem and proof given below.
Theorem 1
Consider two variables, v and u which are relatively prime positive integers and along with it they are reasonably odd by satisfying the condition u > v.
Let us take into account another set of variables, a, b, and c, where a = 2uv, b = u2 – v2 , and c = u2 + v2 , where it is already provided that gcd (a, b, c) = 1 and c2 = a2 + b2 .
If referred to one of the prominent books, Arithmetica written by Diophantus, very elucidated and authentic proof for this theorem could be observed. This proof had led to one of the prominent and path-breaking discoveries in the discipline of number theory which was later termed as Fermat’s last theorem. Below is provided the general and simplified statement of Fermat’s last theorem.
Theorem 2:
Fermat’s Last Theorem: If taken into account the following theorem there would be no solution for the algebraic triplets (X, Y, Z) or integers.
XP + YP + ZP = 0
Provided that the XYZ ≠ 0 and P ≥ 3 is a prime.
The French mathematician Pierre de Fermat had mentioned in his theorem that the segregation of the cube is not feasible and any variable having the power greater than two could not be segregated into equal parts of the same degree.
In the modern era, the Pythagorean theorem is not only used by the mathematicians but also the businessmen and artists. Though the Pythagoras theorem formula is still considered to be the most prominent, relevant, powerful, complex, intellectual, and perplexed ideology in mathematics.
Let us have a look at some of the theorems derived from the Pythagoras theorem formula
Distance Formula
As per this theory, the formula of the distance could be mentioned as
D = d=∆x2 + ∆y2
Where the variable x = x1 – x2 and y = y1 – y2
If the provided distance formula is squared on either side, then you would come up with the Pythagoras theorem formula, which is
D2 = x2 + y2
Cosine Law
The cosine theorem is the most prominent and crucial theorem which was derived out of the Pythagoras theorem formula. By implying the law of cosine, anyone could find the third side if the other two sides are given along with the angle entailed between them. Below is provided the formula to be followed in the cosine law.
c2= a2+ b2– 2ab cos γ
where the variables a, b, and c denote the length of the sides of the provided triangle and y is the value of the angle created in between the two sides i.e. between a and b hence opposite to the side c.
The cosine would consequentially turn out to be zero if the angle y opposite to the side c and in between the sides a and b to be a right angle.
This would satisfy the Pythagoras theorem formula c2 = a2 + b2
Below are given some examples of problems.
Problem 1
Consider a right triangle angled with height 5 m and base 12 m. Calculate the length if hypotenuse of the same right-angled triangle.
Answer:
If referred to the Pythagoras theorem formulas, the equation could be represented by
C2 = A2 + B2
C2 = 52 + 122 = 25 + 144 = 169
C = 13 m.
Problem 2
Consider a right-angled triangle with the length of its hypotenuse 55 m and its altitude as 10 m. Calculate the length of its hypotenuse by calculating the given values.
Answer:
Stating the Pythagoras theorem formula,
C2 = A2 +B2
If derived out the equation for the base from this Pythagoras theorem formula, then it would be
B2 = C2 – A2
B = √ (552 – 102) = 54.083 m
Problem 3
Imagine a right-angled Δ ABC with its hypotenuse of length 50 m and length of the base 30 m. Calculate the altitude or the perpendicular height of Δ ABC.
Answer
While implying the Pythagoras theorem in this context, the below formula could be implemented
C2 = A2 + B2
To deduct the perpendicular height from the above equation, we could imply that
A2 = C2 – B2
A = √ (C2 – B2)
Hence if implied the values in this expression
A = √ (502 – 302)
= √ 900 = 30
Problem 4
By taking into account the length of all the sides of the triangle, determine whether it is a right-angled triangle.
AC = 75, BA = 45, CB = 55.
Answer:
To determine whether the triangle is right-angled, you should prove that the given values of the sides should satisfy the Pythagoras theorem. If considered the sides of a right-angled triangle, the side with the greatest sides should be the hypotenuse. Hence the greatest side would be AC, having the length 75. Let us take the side BA with length 45 as the perpendicular height of the triangle ABC.
Restating the Pythagoras theorem, the below problem could be implied
c2 = a2 + b2
c2 = 752 = 5625
a2 + b2 = 452 + 552
= 2025 + 3025 = 5050
Hence, c2 ≠ a2 + b2 Thus, it could be said that the triangle ABC is not right-angled.
Problem 5
As done in the previous question determine the authenticity of the statement that the triangle ABC is a right-angled triangle, by considering the length of its sides.
RP = 45, QP = 28, and RQ = 53.
Implying the Pythagoras theorem formula,
C2 = A2 + B2
A2 + B2 = 282 + 452= 784 + 2025 = 2809
C2 = 532 = 2809
Hence it is proven that the Pythagoras theorem formula C2 = A2 + B2 could be implied in this context and triangle ABC is actually a right-angled triangle.