As you are aware, pyramids are one of the oldest structures constructed by the human. Ever wondered how much volume a pyramid takes up? Ever give a thought about how it is structured? Do you know how to find the volume of a square pyramid? This paper shall give you guidelines on how to find the volume of a square pyramid.
Definition and History of Pyramid
Pyramid in geometry are solid three dimensions with flat polygonal faces, straight edges and vertices. They are also known as polyhedron (Greek) connected to a polygonal base and a point, known as a vertex. Each of the base edge and vertex forms a triangle, called the lateral face which forms of a conical shape with a polygonal base.
A pyramid with n-sided base has
- n+1 vertices
- n+1 faces
- 2n edges
A well-structured pyramid has its vertex directly above the geometric center of its base. A regular pyramid having a regular polygonal base is usually referred to as a Right Pyramid whereas non-right pyramids are referred as oblique pyramids. When unspecified, a pyramid is generally considered as a Square Pyramid. A square pyramid is generally a pyramid having a square base and the vertex is perpendicular to the center of the square base. If all the faces of the pyramid are equal then it is said to be an equilateral square pyramid.
The geometry of pyramid all started from the ancient Egypt and Babylon, which later developed in ancient Greece. The volume of all the pyramids including the square pyramid was only known to the ancient Egyptians. Democritus was the first Greek mathematician who figured out how to find the volume of a square pyramid.
Types of Pyramids
Many types of pyramids are classified by their type of base. There are various types of pyramids listed below:
- Triangular Pyramid: These are the pyramids that have a triangle as its base.
- Square Pyramid: These are the pyramids that have a square as its base.
- Pentagonal Pyramid: These are the pyramids that have a pentagon as its base.
- Right Pyramid: These are the pyramids that have the vertex of the pyramid directly above the center of its base.
- Oblique Pyramid: These are the pyramids that don’t have their vertex of the pyramid directly above center of its base.
- Regular Pyramid: These are the pyramids that have a regular polygon as its base.
- Irregular Pyramid: These are the pyramids that have an irregular polygon as its base.
Square Pyramid and its Volume
In a square pyramid, the base of the pyramid is of square shape with triangular side faces. The vertex of the pyramid is intended to cast upon the center of the square base.
The volume of any pyramid can be calculated by the given expression
V= 1∕3 Bh
B is the area of square base and h is the height of the square pyramid.
Now, Let us consider the side of the square base is ‘b’ and the height of the square base is ‘h’, then the Area of the base will be B=b2 and the volume of a square pyramid will be given as
V=1/3b2h
This formula can be used to determine the volume of all the sizes of the square pyramid.
- How to find the volume of a square pyramid
- Measure the side length of the base: All the sides of the square are equal in length, thus, measure one side length of the square base and follow these steps.
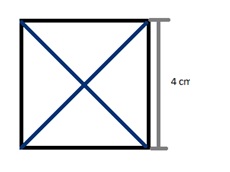
- Let us consider a square pyramid whose base side length is b = 4 cm. as shown in the figure, the value is needed to find the area of the square base.
- Calculate the area of the base: As you’ve found out the side length of the square base of the square pyramid,
- Now, the area of the square base will be the square of the side length of the base i.e. b2.
This can be achieved by multiplying the value of base length twice with itself.b = b x b
b = 4 x 4 = 16 cm2
- Always remember that the dimensions will be expressed as the square units as square centimeters, square meters, square millimeter and so on.
- Now, the area of the square base will be the square of the side length of the base i.e. b2.
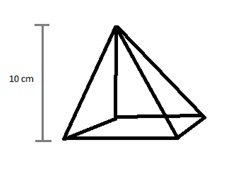
- Measure the pyramid’s height and multiply it with the area of the base: To find out the height of the pyramid measure the length from the base to the vertex of the pyramid at a perpendicular angle.
-
- Now, the height of the pyramid is 10 cm. multiply the area of the base with height as follows:
V =b x h
16 cm2 x 10 cm = 160 cm3
- Now, the height of the pyramid is 10 cm. multiply the area of the base with height as follows:
- Always remember that the volume is always expressed in cubic units.
-
- Obtain the actual volume by dividing the answer by 3: The value which was obtained by multiplying the value of height and area of the base, divide the answer by 3 to get the volume of the square pyramid.
- By dividing 160 cm3 by 3, we get 53.33 cm3the volume for the square pyramid.
- Measure the side length of the base: All the sides of the square are equal in length, thus, measure one side length of the square base and follow these steps.
- Find the volume of the square pyramid by using Slant Height
- Measure the slant of the pyramid: If someone asked you if you knew how to find the volume of the square pyramid but you don’t know the measurement of the pyramid’s height, there is another way to find the volume. That is; by using slant height. Using slant height, you’ll be able to use Pythagorean Theorem to obtain the perpendicular height of the pyramid which can be used to answering the question of how to find the volume of a square pyramid later.
-
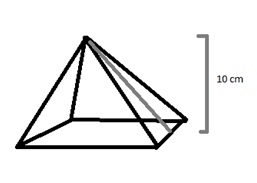
- The Slant height of the pyramid can be referred as the distance from the vertex to the midpoint of one of the base sides. Taking the distance from the corners to the vertex will not be considered as the slant height. Let us consider the slant height of the pyramid as l. Let us assume the value of slant height of the pyramid is 10 cm.
- The Slant height of the pyramid can be referred as the distance from the vertex to the midpoint of one of the base sides. Taking the distance from the corners to the vertex will not be considered as the slant height. Let us consider the slant height of the pyramid as l. Let us assume the value of slant height of the pyramid is 10 cm.
- After measuring the slant height of the pyramid the next step would be creating a virtual right angle triangle.
-
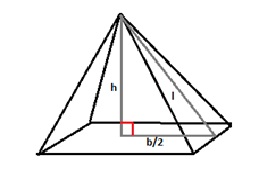
- Visualize the right angle triangle: The next step is to imagine a right angle triangle which is perpendicular and starts from the midpoint of the square base to the vertex. So the l would be the slant height which has been obtained and the base of the right angle is one half of the side length of the square base.Let us assume the side length of the square base is 10 cm, then half of the length would be 5 cm. 5 cm is the base of the right triangle which we have imagined. Using this value in Pythagorean Theorem, we can determine the height of the pyramid.
Pythagorean Theorem uses three variables a, b and c and the formula for Pythagorean Theorem is given as:
a2 + b2 = c2
By assigning the values which we have considered the equation would become
h2 + (b/2)2 = l2Where h is the perpendicular height of the right triangle, b/2 is the base length of the right triangle and l is the slant height of the right triangle. - Solve the Pythagorean Theorem for the value of h: To obtain the value of h, solve the equation and calculate the value the h.
b/2=5 cm l=10 cm
h2 + (b/2)2 = l2
h=√l2– (b/2)2
h=√102 – 52
h=√100 – 25
h=√75
h=8.66 cm
8.66 cm is the perpendicular height of the pyramid from the center of the square base to the vertex of the pyramid. The value of h is needed to find out the volume of the square pyramid.
- Calculate the volume of the square pyramid by using height and base: After using the Pythagorean Theorem, we’ve obtained the height of the pyramid and we already know the side length of the square base. All we need is to apply these values and calculate the volume of the square pyramid.
b= 10 cm h=8.66 cm
v = 1/3b2h
v = (1/3)*(10)28.66
v = 1/3 100 x 8.66
v = (1/3)*(866)
v = 288.66 cm3
- Measure the slant of the pyramid: If someone asked you if you knew how to find the volume of the square pyramid but you don’t know the measurement of the pyramid’s height, there is another way to find the volume. That is; by using slant height. Using slant height, you’ll be able to use Pythagorean Theorem to obtain the perpendicular height of the pyramid which can be used to answering the question of how to find the volume of a square pyramid later.
The volume of the square pyramid is obtained using the slant height of the pyramid. This will really help you to find the volume of the square pyramid if you don’t know the height of the square pyramid. So the next time someone asks you, if you know how to find the volume of a square pyramid, you will know the answer, won’t you.




 Pythagorean Theorem uses three variables a, b and c and the formula for Pythagorean Theorem is given as:
Pythagorean Theorem uses three variables a, b and c and the formula for Pythagorean Theorem is given as:



