Cone Volume: It’s Significance In The Practical World

Cone
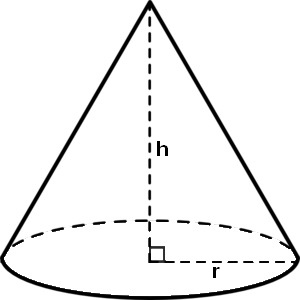
A three-dimensional geometric figure, which retains a flat base though possess a curved later surface having a pointed top is termed to be a cone. The pointed section of the cone at the top is termed as the apex. Below is provided a graphical representation of the cone. Let us have a detailed look over it.
We have to take into account two major mathematical measures while considering cone volume, which is: – Height and its base radius. It should also be noted that a cone has
- Only one vertex and hence has only vertex.
- Zero edges
- One circular face
While considering a cone, the attributes of Altitude and Axis should also be taken into account.
Altitude: The overall perpendicular distance between the base of the cone and apex point is termed to be the altitude of the cone. This measure could also be denoted as the height of the cone
Axis: The distance between the apex and the center of the circular base could be termed as the axis.
In our practical life, we are well aware of various geographical figures. These include two-dimensional figures like square, rectangle, parallelograms, triangles, etc. and three-dimensional figures like a cone, sphere, cylinders, etc. The figures having flat surfaces would come under the division of polyhedral, which include figures like a triangular prism, rectangular prisms, etc. Though the figures like spheres, cones, cylinders could be classified under this division since they retain curved surfaces.
Since this article is intended to focus upon cone, let us concentrate our further discussion over it. If taking a cross-section of a cone, it would resemble an exact two-dimensional triangle. There are a lot of similarities between a cone and a triangle. The major difference which makes a cone unique one from that of a triangle is the presence of a circular base. The vertex of the cone doesn’t need to be on the exact top of the center of the circular base. One of the most common examples of the geometrical figure “cone” is an ice cream cone. It depends upon the base area and altitude of the cone on which its volume depends upon. It is being widely debated that the shape of the cone highly resembles the shape of a pyramid.
The mathematical formula to calculate the volume of a cone is (1/3) Base Area, X Height. A formula is a simplified form and the accurate form of finding the volume of a cone is V = (1/ 3) π r2 h. It is derived from the fact that the area of the circular base is π r2.
There may be a genuine doubt among the readers that what is the major intend behind calculating the cone volume. The major intent is to calculate the actual amount of substance that could be entailed in the given space. In simple words, if a person wants to fill up a huge cone figure, he would have to understand and calculate the cone volume so that amount of required matter could be calculated.
There is no other substitute and simpler way to calculate the volume of a con in the present scenario. In the provided approach has to look at the radius measurement of the circular base of the given cone. The best way of calculating the radius is just finding the diameter of the circular base and diving it into half. When you have measured the radius of the provided cone, you could easily find the base radius by using the formula of π r2. You have to multiply the value of radius with itself to find its square and then you have to calculate the resultant number with the value of π. It is only after this process that the altitude of the cone is taken into account to calculate the Cone Volume. If the height or the altitude of the cone does not provide beforehand them you have to measure the perpendicular distance from the base to the apex by using a scale. The numerical value of the base area of the cone should be multiplied with the (1/3)rd of the height of the cone.
Certain precautions should be taken by the student while calculating the cone volume. The accuracy of the numerical measures regarding all the attributes of the cone should be checked. If the provided measurements of the cone are provided falsely, it would surely affect the accuracy of the calculated volume. Secondly, the student should imply the formula for finding the Cone Volume in a very accurate way. If the formula for cone volume is not byhearted by the student, it is quite probable that he would apply it incorrectly. To calculate the cone volume accurately, the student should maintain accuracy both in the numerical measurements and implication of mathematical formula. The units of measurements should also be kept accurate by the student, otherwise, the evaluator would mark the answer as a false one in the examination. If these factors are kept in mind by the student, he would easily calculate the cone volume without many restrictions.
While moving on with the detailed discussion regarding the cone volume, you should also understand various types of cones so that various aspects and hindrances in calculating the volume should be understood. In the below section of this report on cone volume, different types of cones have listed down, let us have a detailed look over it.
- Inscribed cone
- Circumscribed cone
- Right circular cone
- Oblique Cone
The context in the above section of this report on cone volume could be related to the right circular cone. The volume of the right circular cone could be calculated by the formula, V = (1/ 3) π r2 h
The majority of the cones found in our practical lives are right circular cone. Thee major feature is that the apex is directly situated over the top of the center of the base circle. The base would observe to be flat and two dimensional. If the apex is not situated accurately over the top of the center of the circular base, then the cone would come under the classification of an oblique cone. Based on the shape and the existing circumstances, the cone could also be classified into a Circumscribed cone and an Inscribed cone where the calculation of the volume would be through a much different method. These types of cones should be understood by the student so that the accuracy should be maintained in the calculation of cone volume.
Scope of the cone in the present scenario: It has been observed that most of the popular mass is unaware of the scope and implication of cone volume in the practical scenario. Though the actual measures and dimensions of the cone are very hard to be estimated, their examples could be widely observed in the practical environment. Whether it be the cone of ice cream or a funnel, the shape of the cone could be seen widely in our surroundings.
In the context of chemical or biological labs, various vessels and funnels could be seen in the laboratory and are very crucial to measure the volume contained in it. Any error in the quantity would make a drastic variation and inconsistencies in the result. In many cases, you may have to calculate the volume of the funnel to maintain the accuracy in the measurement.
You may also observe that most of the hills and humans are in the shape of a cone. The base of the geographical figures is often observed to be signifying the shape of a circle. If the person is provided with the accurate height and radius of the mountain, he could easily calculate the volume of that particular mountain. The approach of calculating the volume should be accurate in this context and for this, the person should have the knowledge of various kinds of cones. The approach of calculating the volume of the cone would vary from instance to instance. The person who has a higher level of observation towards his surroundings could find a much more practical implication of the cone.
Even the smaller subjects in our daily life would resemble the shape of a cone. Substances like a funnel, pen caps, rooftops of some buildings, etc. resemble a cone. Though it could be noted that the shape of the cone is not perceived as an attractive figure by the human mind. Since much more basic shapes are stressed upon in the lower classes, kids find it hard to identify the shape of a cone. It is in the large of the academic career that the students are introduced with the concept of cone volume.
If taken into account the ancient culture of Sumerians, the traces of cones could be observed in their counting systems. The clay representations of the cone have been traced down in the geographical positions where the Sumerian culture has existed. It has been derived that the sphere shapes were used to signify the number 10 whereas the cone shapes were used to signify the cone shape. In the Sumerian culture, the large numbers were divided into the multiples of 60 since it has a lot of factors. This is one of the unique numbers which could be divided by consecutive numbers of 1, 2, 3, 4, 5, and 6. The circular figure to signify zero was derived out by the Babylonians. If looked back into the human civilizations, the cone figure had a lot of significance. Though the concept of cone volume was not traced in the ancient human civilizations.
If taken the current situation, the concept of cones is introduced to the students at the very earlier stage of their academic career. It is the duty of the tutors to effectively describe the concepts of the cone volume to their students. It is very important since a lot of the principles in mathematics and engineering are strongly related to the cone volume principles. There should be made some innovative changes in the educational programs so that the concepts of the cone volume should be made much more familiar and thorough to the students. The major reason behind the inability of the students to understand the math principles is the boredom associated with its study. The exact representation of the figures and numerical would create boredom and hence much more practical implications should be introduced in the classroom. The students should understand that there is no middle ground in the subject of mathematics and hence the answer could be either true or false.
Since the educational approach in the schools is achieving higher standards, the student requires much-limited help from online assignment help services. Though just reciting the mathematical formulae would keep aside the students from the actual concept and hence make the whole study process a hard and complex one. The recitation of the formula would help in calculating the cone volume in an emergency though it would not help the person in overcoming the challenging situation where the provided context would differ even a little bit from the recited formula. A critical approach should be taken while discussing the concepts of the cone volume which would make the students much closer to it and discover all the required aspects of it. The students should be provided with the reflective and critical essays so that they could provide their innovative aspects regarding the cone volume. The problems regarding mathematics are very customized and unique one and hence the solution for it could not be just obtained by searching online. Only the accurate implication of the formula and efficient mathematic calculations would help in solving the problems
It is still not clear that who has derived out the formula to calculate the volume of a cone. Though it is one of the basic formulae which has to lead to the derivation of groundbreaking theories in the field of mathematics.