Solving And Understanding Cartesian Equation

Not every student likes being taught mathematics and when it is a compulsory subject, you are filled with anxiety on how to solve the problems and the equations specially the Cartesian equation. Students pursuing mathematics as a full-fledged course are supposed to write and submit assignments based on Cartesian equations. It becomes a problem for students who have less or average knowledge about the basic theories associated with Cartesian equation. Reading the complex theories and trying to understand the equation and its implications makes them puzzled. When these students are asked to submit a Cartesian based assignment, they tremble or become cold. The paper will help you in understanding the Cartesian equation with reference to certain examples.
Understanding the Cartesian equation and its development
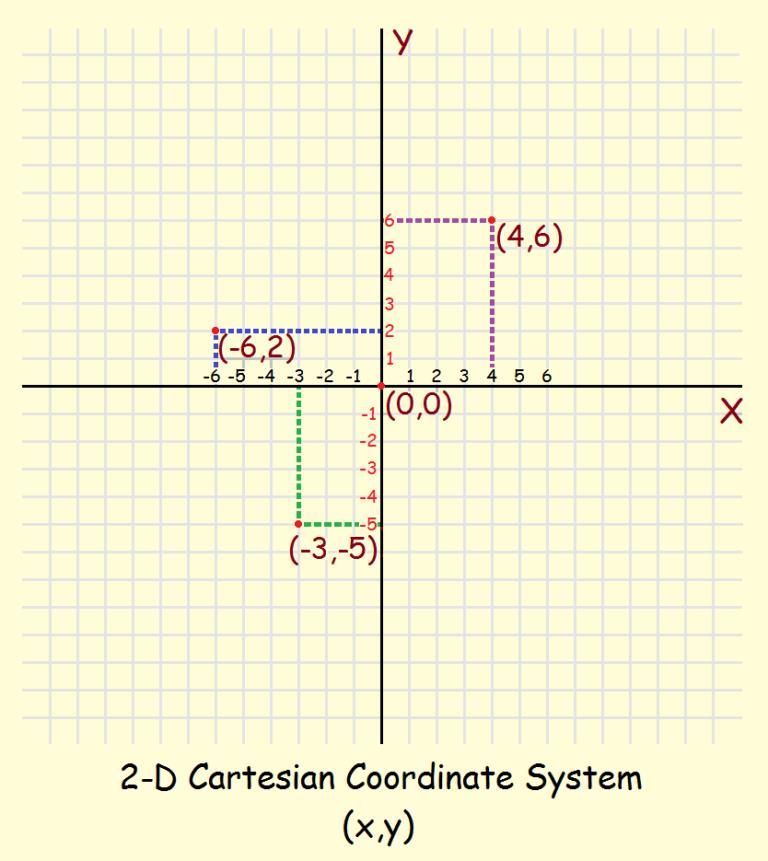
Cartesian equation is the equation of a surface or a curve. The point on the surface or the curve of the Cartesian coordinate is the variables. Rene Descartes who was a philosopher and mathematician in France, coined the word Cartesian in a book which was published in the year 1637. Soon after its discovery, it established an orderly connection between algebra and Euclidean geometry bringing a change in the mathematical world. The growth of Cartesian equation played an important role in the progression of calculus. The plane has been explained basis two coordinate and later assessed in the vector spaces theory. The system of Cartesian coordinate in mathematics is majorly used to determine the points in a plane basis two points named as x and y coordinates. To understand the coordinates, two lines are drawn perpendicular to each other having x and y axis. The marking of the axes is shown below:
The vertically placed line signifies y axis and the horizontal line is the x axis. The axes can be used to give value to the points. The intersection point of the graph is known as zero point or point of origin. It can be seen that the equation of Cartesian in the graph presents
What are the steps to interchange polar equation and Cartesian equation?
Understanding the polar equations and solving questions related to it can be tough for students and they can be discouraged and leave their dream of becoming a nuclear physicist. But there are certain easy steps which can help in understanding the interchange of both polar equation and Cartesian equation.
Form identification of the equation: In case an equation has rs andƟs then it is an easy indication that it is in a polar form. If the equation has xs and ys then it indicates the Cartesian form.
Clear objective: If you are given a task to convert polar equation to Cartesian equation then you first need to change the equation inputs in order to be left with xs and ys. If you are asked to change the latter into former then you will have to somehow bring the equation inputs to rs andƟs. If you get stuck while converting the equation, don’t panic, take some fresh air, refresh your mind and restart the process.
Read the equation: You need to thoroughly check the equation before solving it. Try to find out the important elements of the equation. If the elements that you were searching for is not present in the equation then you need think of ways in order to add them. In case the given equation is in polar form then search for r²=or rcos(Ɵ)=or rsin(Ɵ)= but in case of Cartesian equation then look for x²+y² or x or y. Once you have found the required elements, start substituting.
Merge terms which are like or complete the squares: In case you have squares in the equation, try to complete it. When you have solved the equation, the inputs will reflect r in place of Ɵ or y n place of x. The change can only take place once you have simplified and combined the terms.
Following the above steps, polar can be changed to Cartesian equation or vice-versa. In case you are still stuck in between then you can take help from some online calculators which have been made to solve such equations.
Converting parametric equation to Cartesian equation
Sometimes a student can be asked to search a Cartesian equation of a curve by removing the parameters. The conversion can be explained with the help of the below equation:
x(t)=t²+1 and y(t)=2+t
For the above equations, the parameter is to be first eliminated and the equation parametric equation has to be written as Cartesian equation.
Let’s us start with y as it is easy to solve the equation with t.
y=2+t
y-2=t
Now replace y-2 for t in x(t).
x=t2+1
x=(y-2)2+1 Replace t into x
x=y²-4y+4+1
x=y²-4y+5
Therefore x=y²-4y+5 is the Cartesian equation.
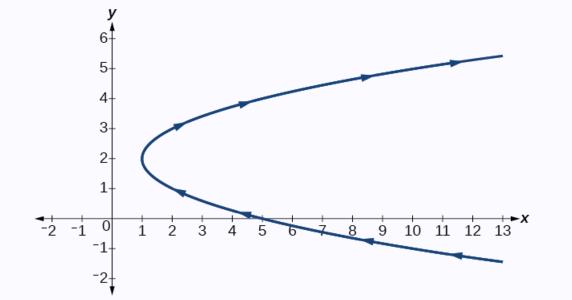
The equation is for a parabola and in the rectangle terms it can be seen that x depends on y. We can see in the below diagram, at the vertex of the curve (1,2), the graph shifts to the right. It can be considered that the functions of the given equations, x(t) and y(t), t which is time is an independent variable. It can be noted that x and y are both functions of time which leads to the fact that generally y cannot be considered as a function of x.
Parabola and parametric equation
Finding the parametric equation of a parabola is very simple. Coordinates of any point can be easily represented on parabola in the form of y²=4ax is (a^2,2at). We can see that (a^2,2at) satisfies the parabola equation for y²=4ax for each value of t. Joining the equation x=at² andy=2at, having the parameter as t are known as parametric equation of a parabolay²=4ax.
There are other standards as well of parabola which are discussed below
1. The standard equation of parabola is y²=-4ax:
- The parametric coordinates of the parabola y²=-4ax are (-at2,2at).
- Parametric equations of parabola y²=-4ax are x=-at2,y=2at.
2. The standard equation of parabola x²=4ay:
- The parametric coordinates of the parabola x²=4ay are (2at,at2).
- Parametric equations of parabola x²=4ay are x=2at,y=at².
3. The standard equation of parabola x²=-4ay:
- The parametric coordinates of the parabola x²=-4ay are (2at,-at2).
- Parametric equations of parabola x²=-4ay are x=2at,y=-at².
4. The standard equation of parabola (y-k)2=4a(x-h):
- Parametric equations of parabola (y-k)2=4a(x-h)are x=h+at² and y=k+2at.
Let us solve an equation in order to get a clear understanding. Suppose you are given with y²=12x parabola and you need to find the parametric equation. The equation y²=12x can take the form of y²=4ax. When the equation y²=12x is compared with y²=4ax it brings out 4a=12⇒a=3. It can be seen that x=3t² and y=6t is the parametric equation of the parabola.
Solving Cartesian equation of a curve
To solve the Cartesian equation of a curve is not an easy task. Students who are unable to solve it take help from online calculators. The below e.g. can guide you in solving the Cartesian equation:
Suppose x=2+t² and y=4t is the parametric equation of a curve and now you needed to find Cartesian equation of the curve. You need to simply find a single equation for the curve as per regular criteria wherein there are two variables, xs and ys.
First finding the parametric equation:
It is stated that y=4t now you need to divide the two sides by 4 to get (1/4)y=t.
The new value can be replaced in the equation for x:
x=2+(1/4(y))²=t
Expanding the brackets just square 1/4 and y, you will get x=2+1/16y².
Ideally, the equation has already taken the Cartesian form due to the inclusion of x and y variables but further change in positioning is required to get the standard y=form:
x=2+1/16y² deduction of 2 is from both sides
x-2=1/16y² each side has to be multiplied by 16
16x-32=y² squaring both sides you get y=SQRT(16x-32).
Solving equation of level curve
A function’s level curve is a point curve, in which it integrates constant values. A cross section of the equation graph is considered as the level curve. If it is equaled to some constant values, such as a function of two variables lets say x and y, then you will consider the point curve (x , y), where the equation has a constant value.
Let’s explain the logic with an e.g.:
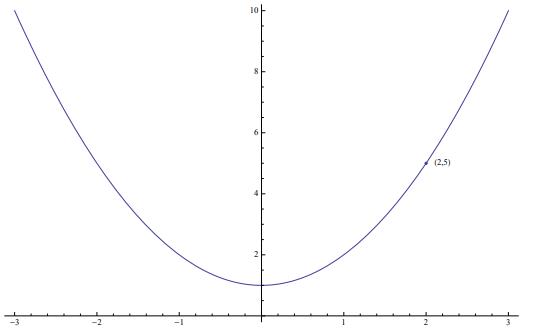
Function to consider is f(x,y)=e y-x 2-1 and you need to get the equation of level curve f which passes the point (2,5) along with a sketch of the curve.
Consideringf(x,y)=e 5-2 2-1 = e 0 = 1, the level curve having (5,2) is said to be the curve f(x,y)=1.
The application of equation e y-x 2-1 at both the sides, the equation can be re-written as y-x^2-1=0 or y=x^2+1 as per its level curve.
The below graph provides the view of the solved level curve.
Dimensions of Cartesian equation
Cartesian equation has different dimensions which are being discussed hereinafter:
One dimensional: Cartesian coordinate for one dimensional space is basically for a straight line. A point O from the origin is selected on the line along with the length unit and an orientation. Orientation helps in selecting the positive and negative among the two lines with the help of point O. The number line is the chosen line for the Cartesian system. The line has real numbers located at a particular location and the organization of each point can be clearly understood.
Two dimensional: Cartesian coordinate for two dimensional has an organized pair of perpendicular axis. The length has a single unit for both pairs along with an aligned axis. The meeting point of the axes is called as origin having number line on each axis.
Three dimensional: Cartesian coordinate for three dimensional consists of three axes. They walk at a common point pairing perpendicular having orientation and a single unit for each axis. The three numbers chosen are the Cartesian relates of P and P is regulated by opposite construction in three coordinates.
We hope that the contents of the article will help in overcoming the challenges which most students face when given a task to solve the Cartesian equation. Applying the easy steps discussed in the aforementioned paragraphs will help completing assignments. In case a student still fears to solve assignments related to mathematics, reach out to Totalassignmenthelp.com. Our Mathematics assignment help is here to take all your fears and give you a peace of mind.
Totalassignmenthelp.com has a set of writers who are brilliant and quick in solving equations, be it polar, Cartesian or any other. They have been chosen after a thorough check which includes their study, experience and the way they handle deadlines. The third category has been included as we are aware that meeting deadlines is an important aspect in a student’s life. It is always our priority to deliver assignments on time so that if in case the student has any concern after having a look at the assignment, we are there to help him. We not only solve polar or Cartesian equations but we also provide services related to different other topics that you find in mathematics like algebra, calculus, trigonometry, geometry, etc. We are also into making different other assignments related to almost all subjects. You can have a look at the type of assignments being made by us on our website. The assignments being delivered not only meet the quality and correctness parameters but it is also available at reasonable rates, so don’t wait, contact us immediately.